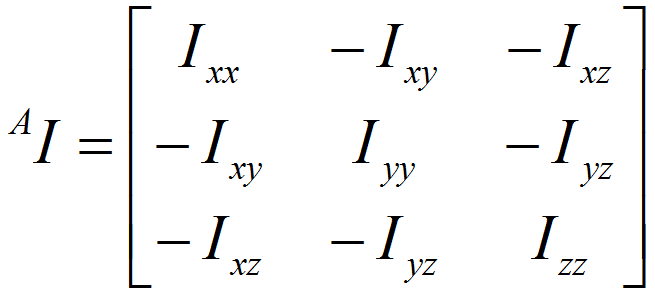
黄杰, 2013-06-10
root[a]linuxsand.info
tags: robotics
原书目录:
在任一瞬时,对刚体的线速度和角速度进行求导,可分别得到线加速度和角加速度。
在单自由度系统中,常常需要考虑刚体的质量。对于定轴转动的情况,经常用到 惯量矩 这个概念。在一个刚体绕任意轴作旋转运动时,需要一种能够表征刚体质量分布的方法,于是引入 惯性张量,它可以被看作是对一个物体惯量的广义度量。
坐标系{A}中的惯性张量可表示如下:
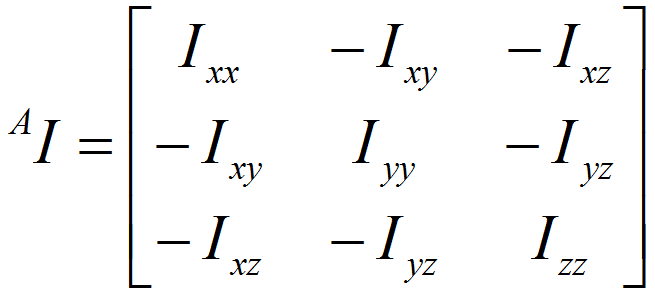
当任意选择坐标系方位时,可能会使刚体的惯量积为零。此时,参考坐标系的轴被称为主轴,而相应的惯量矩被称为主惯量矩。
惯性张量是坐标系位姿的函数,平行移轴定理 就是在参考坐标系平移时惯性张量如何变化的计算方法,它描述了一个以刚体质心为原点的坐标系平移到另一个坐标系时惯性张量的变换关系。
要使连杆运动,必须对连杆进行加速和减速。连杆运动所需的力是关于连杆期望加速度及其质量分布的函数。牛顿方程以及描述旋转运动的欧拉方程描述了力、惯量和加速度之间的关系。
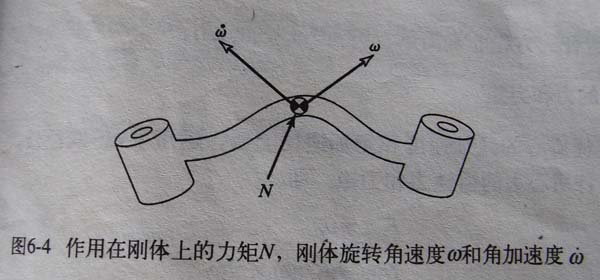
旋转刚体的角速度、角加速度分别为 ω、ω',由欧拉方程可得作用在刚体上的力矩 N 引起刚体的转动为:
N = CIω' + ω × CIω
CI 是刚体在坐标系{C}中的惯性张量,刚体的质心在{C}的原点上。
假设已知关节的位置、速度和加速度,结合机器人运动学和质量分布方面的知识,可以计算出驱动关节运动所需的力矩。
为了计算作用在连杆上的惯性力,需要计算操作臂每个连杆在某一时刻的角速度、线加速度和角加速度。可应用迭代法:首先对连杆 1 进行计算,接着计算下一个连杆,这样一直向外迭代到连杆 n。
计算出每个连杆质心的线加速度和角加速度之后,运动牛顿-欧拉公式便可以计算出作用在连杆质心上的惯性力和力矩。
计算出作用在每个连杆上的力和力矩后,需要计算关节力矩,它们是实际施加在连杆上的力和力矩。
列出力平衡方程和力矩平衡方程。应用这些方程对连杆依次求解,从连杆 n 开始向内迭代一直到机器人基座。
由关节运动计算关节力矩的完整算法由两部分组成。第一部分是对每个连杆应用牛顿-欧拉方程,从连杆 1 到连杆 n 向外迭代计算连杆的速度和加速度。第二部分是从连杆 n 到连杆 1 向内迭代计算连杆间的相互作用力和力矩以及关节驱动力矩。
假想机器人正以 1g 的加速度在做向上加速运动,就可以很简单地将作用在连杆上的重力因素包括到动力学方程中去,不需要其他额外计算就可以对重力影响进行计算。
以平面二连杆操作臂为例,封闭形式的动力学方程。结果很复杂(这才是一个最简单的操作臂啊,可想而知一个封闭形式的六自由度操作臂的动力学方程是多么复杂!)。
有需要会精读,P140 - 143。
牛顿-欧拉方法是基于基本动力学公式以及作用在连杆之间约束力和力矩分析之上的。一个替代的方法是拉格朗日动力学公式。前者是力平衡方法,后者是基于能量的动力学方法。
前述的动力学方程都是按照操作臂关节角(关节空间)对位置和时间的导数建立的。建立关节空间方程的目的是便于应用串联机构的性质推导动力学方程。
原内容将会讨论笛卡尔空间末端执行器的加速度与作用在末端执行器上的笛卡尔空间力和力矩之间关系的动力学方程,此处略过。
上述动力学方程只包含了刚体力学中的那些力,没有包含摩擦力。为了反映实际工况,需要建立摩擦力的模型。
由封闭形式的动力学方程,可通过仿真求出动力学方程中的加速度,然后应用一些数值积分方法对加速度积分,计算出位置和速度。
一种最简单的数值积分方法:欧拉积分。(……)通过输入已知的力矩函数,用数值积分方法即可求出操作臂的位置、速度和加速度。
因为典型操作臂的动力学方程非常复杂,因此必须考虑计算效率问题。(略)