机器人学导论阅读笔记 2 -- 空间描述和变换

黄杰, 2013-06-06
root[a]linuxsand.info

tags: robotics

原书目录：

• 概述
• 描述：位置、姿态与坐标系
• 映射：从坐标系到坐标系的变换
• 算子：平移、旋转和变换
• 总结和说明
• 变换算法
• 变换方程
• 姿态的其他描述方法
• 自由矢量的变换
• 计算分析

世界坐标系

讨论任何问题可以参照的坐标系。

位置描述

用 3 x 1 的位置矢量对世界坐标系中的任何点进行定位。

位置矢量用一个前置的上标来表明其参考的坐标系。或者用矩阵来表示：

姿态描述

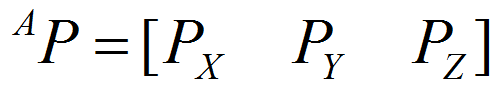
在物体上固定一坐标系并给出此坐标系相对于参考系的表达。

{B} 相对于 {A} 中的描述 -> 姿态旋转矩阵

• 点的位置：一个矢量
• 物体姿态：一个矩阵

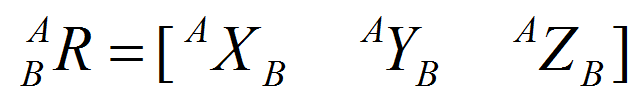
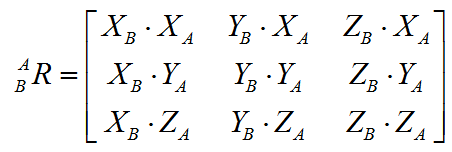
旋转矩阵的各分量：方向余弦

正交矩阵 R，R ^-1 = R ^T

坐标系的描述

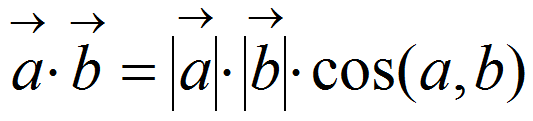
由于位置和姿态经常成对出现，我们将此组合成为「坐标系」。4 个矢量为一组，表示了位置和姿态信息。

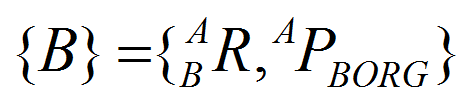
其中，^AP_BORG 是确定 {B} 的原点的位置矢量。

映射：坐标系之间的变换

• 平移（姿态相同）
• 旋转
• 二者结合

平移

可用矢量相加的方法求点 P 相对于 {A} 的表示 ^AP。

旋转

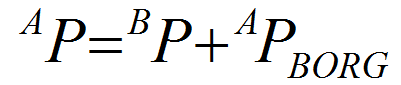
过程在 P18，结果的简化形式：

一般坐标系的变换：

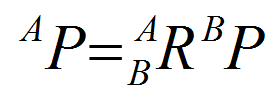
齐次变换矩阵

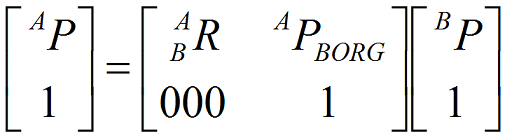
简洁形式（用于公式推导）：

算子

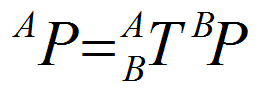
用于坐标系间点的映射的通用数学表达式。

• 平移算子
• 矢量旋转算子
• 平移加旋转算子

具体略过。

总结和说明

齐次变换矩阵：

1. 是坐标系的描述
2. 是变换映射
3. 是变换算子

「坐标系」和「变换」都可用「位置矢量 + 姿态」来描述。一般来说，「坐标系」主要用来描述，「变换」主要用来表示映射或算子。

（略过 2.6 变换算法，2.7 变换方程，2.8 姿态的其它描述方法，2.9 自由矢量的变换，2.10 计算分析）

附，机器人系统的示教和预定义姿态运动。