黄杰, 2013-06-07
root[a]linuxsand.info
tags: robotics
原书目录:
操作臂运动学涉及所有与运动有关的几何参数和时间参数。本章重点:将操作臂关节变量作为自变量,描述操作臂末端执行器的位置和姿态与操作臂基座之间的函数关系。
设计操作臂时,通常优先选择仅具有一个自由度的关节作为连杆的连接方式。典型的操作臂具有 5 或 6 个关节。
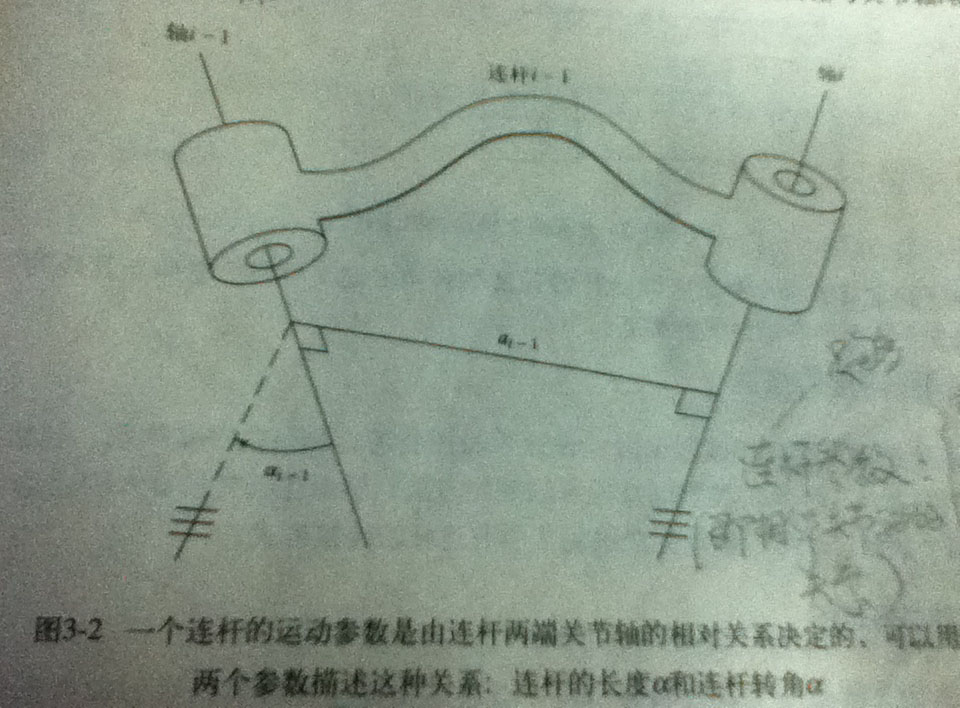
一个连杆的运动参数,可以用两个参数来描述:

注意:
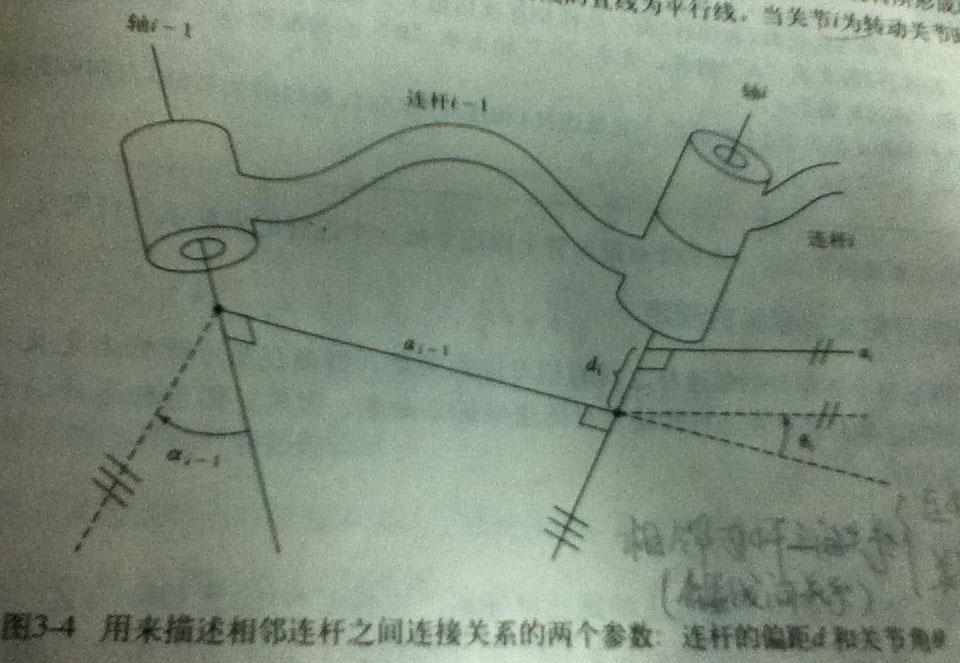
每个连杆都可以用 4 个运动学参数来描述。两个用来描述连杆本身,另外两个用来描述连杆之间的连接关系。
那么,对于转动关节,是一个变量(关节角)三个常量;对于移动关节,也是一个变量(连杆偏距)三个常量。这叫做「Denavit-Hartenberg 参数」。
在每个连杆上定义一个固连坐标系({i}),用来描述相邻连杆之间的相对位置关系。
如何建立连杆坐标系?P53 ~ 54
例题:
RPR 型
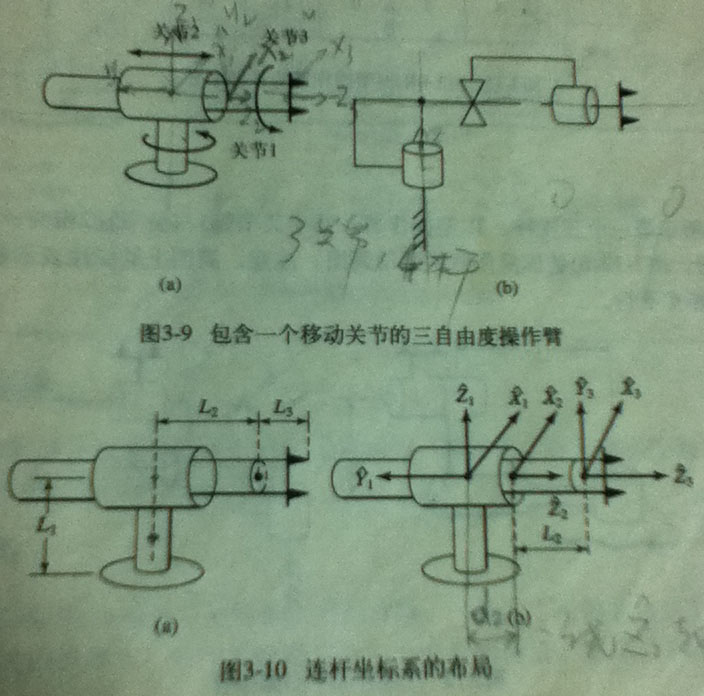
3R 型
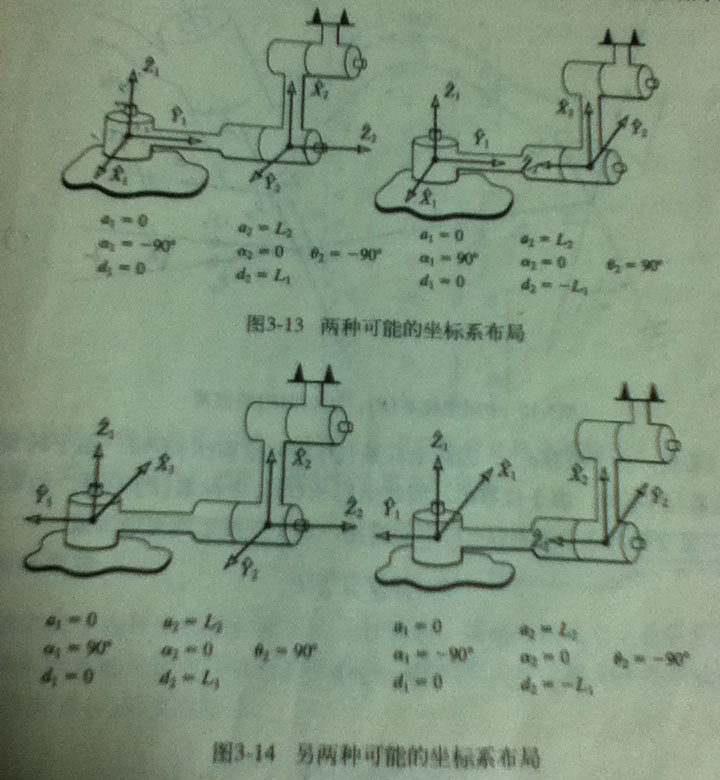
推导出相邻连杆间坐标系变换的一般形式,然后求出连杆 n 相对于连杆 0 的位置和姿态。
公式:
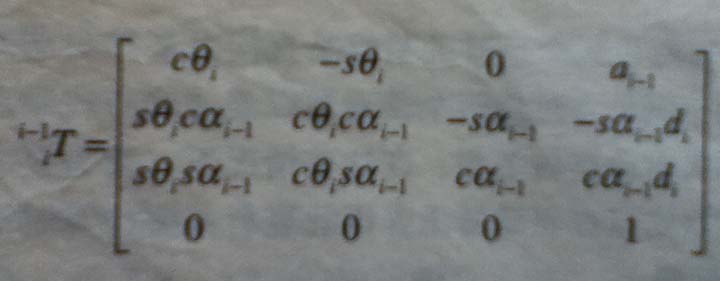
连续的连杆变化:
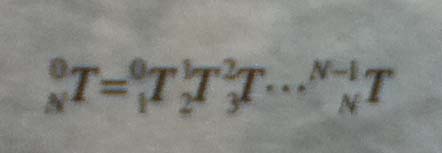
对工业机器人来说,并非每个运动关节都是直接由某种驱动器来驱动(有时是两个驱动器以差动方式驱动一个关节,有时用直线驱动器通过四连杆机构来驱动)。
由于测量操作臂位置的传感器常常安装在驱动器上,因此进行某些计算时必须把关节矢量表示成一组驱动器矢量,即驱动器矢量。
一个操作臂的位置、姿态描述有 3 种表示方法:
在进行机器人设计或分析时,都必须确定驱动器位置和关节位置的对应关系。
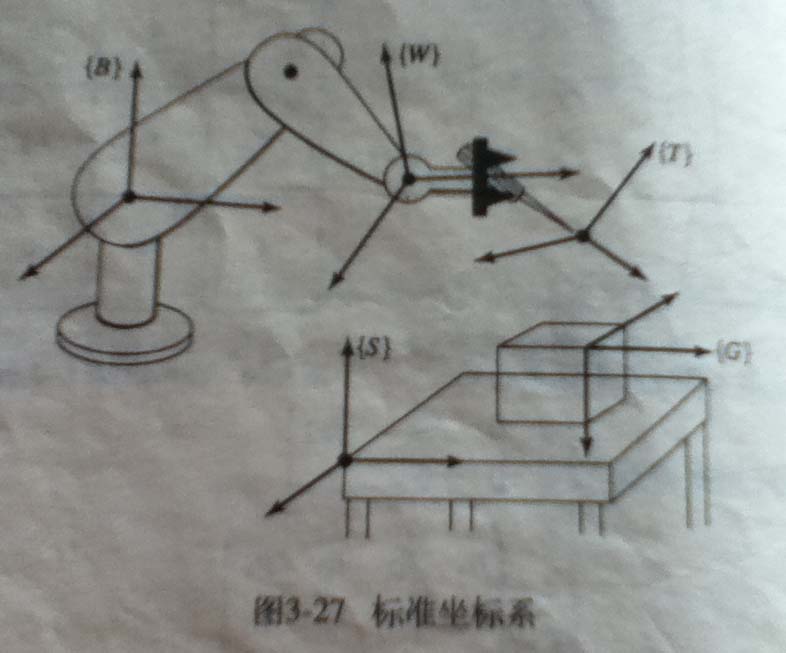
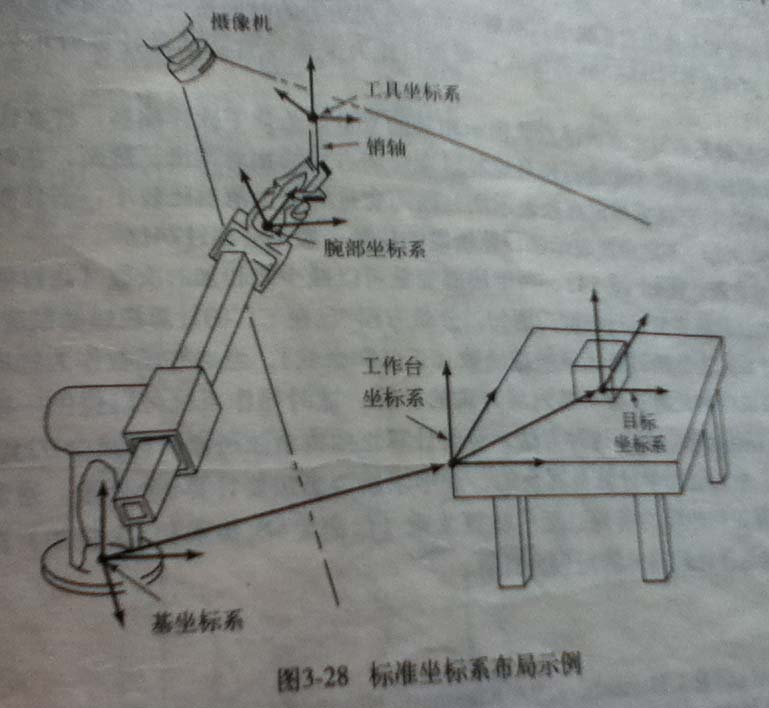
机器人首要功能之一是计算出工具坐标系{T}相对于工作台坐标系{S}的变换矩阵,这便是某些机器人系统中的 WHERE 函数,用来计算手臂的位置。
在实际应用中,求解运动学方程所需的时间是必须考虑的。主要耗时的是计算超越函数(正弦、余弦)。与其利用标准库中的函数来计算,不如把结果以表的形式放在内存中。