机器人学导论阅读笔记 5 -- 速度和静力

黄杰, 2013-06-09
root[a]linuxsand.info

tags: robotics

原书目录：

时变位姿的符号表示

线速度描述了点的一种属性，角速度描述了刚体的一种属性。由于坐标系总是固连在被描述的刚体上，所以可以用角速度（Ω）来描述坐标系的旋转运动。

机器人连杆的运动

一般使用连杆坐标系{0}作为参考系，所以 vi 是连杆坐标系原点{i}的线速度，ωi 是连杆坐标系{i}的角速度。

连杆间的速度传递

「连杆的速度」是指「连杆坐标系原点的线速度」和「连杆的角速度」。连杆 i+1 的速度就是连杆 i 的速度加上那些附加到关节 i+1 上的新的速度分量。

雅可比

雅可比矩阵是多元形式的导数。在机器人学中，通常使用雅可比将关节速度与操作臂末端的笛卡尔速度联系起来。雅可比矩阵的行数 = 操作臂在笛卡尔空间的自由度数量，雅可比矩阵的列数 = 操作臂的关节数量。

奇异性

已知一个线性变换可以将关节速度和笛卡尔速度联系起来，这个线性变换矩阵是可逆（非奇异）的吗？

事实上，大多数操作臂都有使得雅可比矩阵出现奇异的 Θ 值（Θ 是操作臂关节角矢量），这些位置就称为「机构的奇异位形」或「奇异状态」。所有的操作臂在工作空间的边界都存在奇异位形，并且大多数操作臂在它们的工作空间内也有奇异位形。

  1. 工作空间边界：出现在操作臂完全展开或者收回使得末端执行器处于或非常接近工作空间边界的情况
  2. 工作空间内部：出现在远离工作空间的边界，通常是由于两个或两个以上的关节轴共线引起的。

当一个操作臂处于奇异位形时，它会失去一个或多个自由度（在笛卡尔空间中观察），也就是说，在笛卡尔空间的某个方向上（或某个子空间内），无论选择什么样的关节速度，都不能使机器人手臂运动。

作用在操作臂上的静力

场景：操作臂的末端执行器在工作空间推动某个物体，求出保持系统静态平衡的关节扭矩。

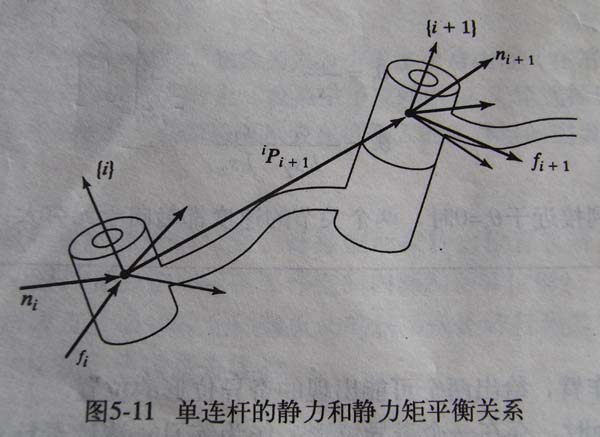
不考虑连杆重力，关节静力和静力矩是由施加在最后一个连杆上的静力或静力矩引起的。