机器人学导论阅读笔记 7 -- 轨迹的生成

黄杰, 2013-06-11
root[a]linuxsand.info

tags: robotics

原书目录：

• 概述
• 关于路径描述和路径生成的综述
• 关节空间规划方法
• 笛卡尔空间规划方法
• 笛卡尔路径的几何问题
• 路径的实时生成
• 使用机器人编程语言描述路径
• 使用动力学模型的路径规划
• 无碰撞路径规划

本章讨论计算轨迹的方法，该轨迹（指：每个自由度的位置、速度和加速度的时间历程）描述了操作臂在多维空间中的期望运动。

为了使机器人系统的用户便于对操作臂的运动进行描述，不应当要求用户必须写出复杂的时间和空间的函数才能指定机器人任务，相反，应该允许用户通过简单的描述来指定机器人的期望运动，然后由系统来完成详细的计算。例如，用户可能只需给定末端执行器期望的目标姿态，而由系统来确定到达目标的准确路径、时间历程、速度曲线等。

此外，规划好的轨迹如何在计算机中中进行 描述 也是一个值得关注的问题。最后，要研究通过内部表达式计算轨迹的问题——即轨迹生成问题。大多数情况下，在轨迹生成的运行时间内需要计算位置、速度和加速度。这些轨迹由数字计算机计算，因此要以某种速率计算轨迹点，此速率叫做 路径更新率。在典型的操作臂系统中，路径更新率在 60HZ 到 200HZ 之间。

关于路径描述和路径生成的综述

将操作臂的运动看作是工具坐标系{T}相对于工作台坐标系{S}的运动，用这种方式描述路径和生成路径是非常有利的。

一个基本问题是将操作臂从初始位置移动到某个最终期望位置——也就是将工具坐标系从当前值{T_initial}移动到最终期望值{T_final}，运动包括工具相对于工作台的姿态变化和位置变化。

有时需要指定运动的更多细节而不只是简单地指定最终的期望位形。一种方法是在路径描述中给出一系列的期望中间点，每个中间点实际上都是确定工具相对于工作台的位置与姿态的坐标系。路径点 = 中间点 + 初始点 + 最终点（「点」= 表示位置、姿态的坐标系）。除去这些空间约束，还可以指定运动的 瞬时属性，如中间点之间的时间间隔。

通常，期望操作臂的运动时平滑的。为此，要定义一个连续的且具有连续一阶导数的光滑函数。有时还希望二阶导数也是连续的。急速的运动会加剧机构的磨损，激起操作臂共振。因此，为了保证路径平滑，必须在各中间点之间，对路径的空间和时间特性给出一些限制条件。任何通过中间点的光滑函数都可以用来指定精确的路径。

关节空间的规划方法

本节将研究以关节角的函数来描述轨迹（在空间和时间）的轨迹生成方法。

应用逆运动学理论，将中间点「转换」成一组期望的关节角。这样，就得到了经过各中间点并终止于目标点的 n 个关节的光滑函数。对于每个关节角而言，由于各路径段所需要的时间是相同的，因此所有的关节将同时到达各中间点，从而得到{T}在每个中间点上的期望的笛卡尔位置。尽管对于每个关节指定了相同的时间间隔，但对于某个特定的关节而言，其期望的关节角函数与其他关节函数无关。

尽管各中间点之间的路径在关节空间中的描述非常简单，但在笛卡尔坐标空间中的描述却很复杂。一般情况下，关节空间的规划方法便于计算，并且由于关节空间与笛卡尔坐标空间之间并不存在连续的对应关系，因而不会发生机构的奇异性问题。

一些方法：

• 三次多项式
• 具有中间点的路径的三次多项式
  • 确定中间点处的期望关节速度可以使用以下几种方法（不展开，见 P165 - 166）：
    1. 根据{T}的笛卡尔线速度和角速度确定每个中间点的瞬时期望速度
    2. 在笛卡尔空间或关节使用适当的启发式方法，系统自动选取中间点的速度
    3. 采用使中间点处的加速度连续的方法，系统自动选取中间点的速度
• 高阶多项式
• 与抛物线拟合的线性函数
• 具有中间点的路径与抛物线拟合的线性函数

笛卡尔空间规划方法

本节讨论的路径生成方法是用笛卡尔位姿关于时间的函数来描述路径形状，此方法可以确定路径点之间的空间路径形状。最常见的路径形状是直线，不过也会使用圆、正弦或其他路径形状。

在基于笛卡尔空间的路径规划方法中，形成轨迹的样条函数是描述笛卡尔变量的随时间变化的函数。这些路径点是由{T}相对于{S}来描述的，无需事先进行逆运动学求解。可是，执行笛卡尔规划的计算量很大，因为在运行时必须以实时更新路径的速度求出运动学逆解。

「笛卡尔直线运动」是一种生成笛卡尔路径的规划方法。

笛卡尔路径的几何问题

由于笛卡尔空间与关节位置之间有连续的对应关系，所以笛卡尔空间的路径容易出现于工作空间和奇异点有关的各种问题。

一：不可达的中间点

在关节空间中从 A 到 B 没有问题，但若试图在笛卡尔空间沿直线运动，将无法到达某些中间点。该例表明在某些情况下，关节空间中的路径容易实现，而笛卡尔空间中的直线路径将无法实现。

二：在奇异点附近的高关节速率

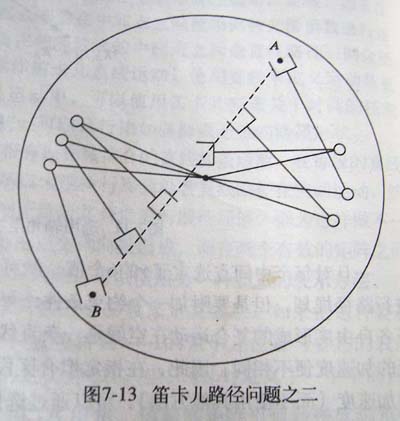
如果一个操作臂沿笛卡尔直线路径接近机构的一个奇异位形时，则机器人的一个或多个关节速度可能增加至无穷大。由于机构的速度是有上限的，因此这通常将导致操作臂偏离期望的路径。

三：不同解下的可达起点和终点

两个杆的长度相同，但关节存在约束，使得机器人到达空间给定点的解的数量减少。

小结：为了处理在笛卡尔空间定义路径存在的这些问题，大多数工业操作臂控制系统都具有关节空间和笛卡尔空间的路径生成功能。用户可以很快明白由于使用笛卡尔空间路径存在一定困难，所以一般默认使用关节空间路径。

路径的实时生成

完整解析方法：

1. 使用逆运动学计算关节的位置
2. 使用逆雅可比矩阵计算关节速度
3. 使用逆雅可比矩阵及其导数计算角加速度

使用机器人编程语言描述路径

使用 AL 语言举例，斯坦福大学开发的机器人编程语言。

假定操作臂从位置 A 开始运动，在关节空间使操作臂沿着带有抛物线拟合的直线路径运动：

move ARM to C with duration = 3*seconds;

以直线移动到相同的位置和姿态：

move ARM to C linearly with duration = 3*seconds;

如果加入一组中间点：

move ARM to C via B,A,D;

在 AL 语言中，可以为某个区段单独指定时间间隔（向 B 点运动的第一个区段的时间间隔为 3s）：

move ARM to C via B where duration = 3*seconds;

使用动力学模型的路径规划

在规划路径时，如果假定在每个关节或沿着每个自由度具有最大的加速度，则意味着做了很大的简化。实际上，为了避免超出驱动设备的承受能力，必须保守地选取最大加速度值。

无碰撞路径规划

如果能做到：已知目标点，让系统自定决定中间点的位置和数量。那么必须要有操作臂的模型、工作区域以及在区域内所有潜在的障碍。如果在该区域内还有第二个操作臂在工作的话，在这种情况下，每个机械臂都应该把对方视为运动的障碍。

无碰撞路径规划目前有两种互相竞争的技术。一是做出一个描述无碰撞空间的连接图，然后在该图中搜索无碰撞路径；然而，其复杂性随着操作臂的关节数量增加而按指数幅度增加。二是在障碍的周围设置人工势场，使操作臂向目标点处的人工引力场运动时避免碰上障碍；然而，它只考虑了局部环境，会在人工势场区域的某个局部极小区被「卡住」。

无碰撞路径规划系统尚未获得商业应用。